Sensitivity Analysis

Sensitivity Analysis and Discounting

In order to ensure that the discount rate (and/or horizon value) used by the researcher is appropriate and is not solely responsible for the outcome of a project appraisal, the researcher may wish to perform a sensitivity analysis. This can be used to improve the robustness of a CBA, and is particularly useful where there is uncertainty over the discount rate.

Testing Sensitivity by varying the Discount Rate and Horizon Value

The researcher may vary the discount rate and the horizon value in order to test the sensitivity of the CBA. This is a particularly simple procedure to complete when using a spreadsheet to conduct a CBA including CBA Builder Simple and Advanced. Projects, whose costs are all incurred early, for example many construction projects, may be especially susceptible to discount rate sensitivity. This is because a higher discount rate reduces the present value of the benefits which are accrued over time, while having no effect on the initial costs involved in the project.

Example

Consider a construction project with initial costs of £1.5m. Benefits arising from this project are £100,000 at the end of year 1, £200,000 at the end of year 2, £500,000 at the end of year 3, and £1m at the end of year 4.

With no discounting the NPV of this project is as follows:

NPV = Benefits - Costs

NPV = £1.7m - £1.5m

NPV = £200,000

With a discount rate of 5% the NPV of the project is as follows:

£95,238.10 + £181,405.90 + £431,918.8 + £822,702.47

NPV (B) = £1,531,265.30

NPV = £1,531,265.30 - £1.5m

NPV = £31,265.30

With a discount rate of 10% however the NPV of the project is as follows:

£90,909.09 + £165,289.26 + £375,657.40 + £683,013.46

NPV (B) = £1,314,869.20

NPV = £1,314,869.20 - £1.5m

NPV = -£185,130.79

In this example without discounting there is economic justification for the project to go ahead. With a discount rate of 5% similarly there is justification for the project to go ahead. However, with a higher discount rate of 10% the costs outweigh the discounted benefits by almost £200,000, suggesting the project should not go ahead. In this case the choice of discount rate could have a significant impact on the viability of the construction project.

Plotting the various outcomes for different discount rates can allow a researcher to arrive at the break even discount rate. This is the rate at which the NPV is equal to zero. This break even rate is, however, influenced by the horizon value. With a horizon value of zero, the break even rate will be naturally lower than with a higher horizon value. In our example, if the project has a horizon value of £200,000 then even a discount rate of 10% will produce a positive NPV.

With a discount rate of 10% and a horizon value of £200,000, the NPV of the project is as follows:

NPV = PV (B) – PV (C) + PV (H)

NPV = £1,314,869.20 - £1.5m + £200,000

NPV = £14,869.21

The Internal Rate of Return

The break even discount rate is sometimes referred to as the Internal Rate of Return (IRR). The value of the break even discount rate or IRR can be used in two ways. It can be used to compare projects. For example, a project with an IRR of 6% is equivalent to another project of IRR 6%, at least in economic terms. This is particularly useful for projects when comparing with a ‘do nothing’ approach. If the IRR value, that is the value at which NPV is equal to zero, is higher than the social discount rate (i.e. the interest rate used in the CBA), then this provides economic justification for the project to go ahead. If, however, the IRR is lower than the social discount rate, this suggests the project should not go ahead.

There are a number of limitations in the use of the IRR. First, it may be the case that there is more than one occasion when the NPV is zero, that is at more than one discount rate or IRR. In addition, the IRR should not be used to select from a range of projects which differ substantially in size. Remember the IRR is a percentage value not a monetary (£) value.

Other Forms of Sensitivity Analysis

In addition to testing for sensitivity relating to discount rate and horizon values, it may also be necessary for the researcher to consider the sensitivity of the CBA to other measures. A range of situations may call for the use of sensitivity analysis of some form. These include exploring the effects associated with changing:

Values given to time.
Wage rates used.
The value of life, or risks associated with certain occupations.
The multiplier effect applied to the economic impact of an investment or scheme.
Environmental impacts.

The researcher must determine how changes in these measures affect the outcome of the CBA. A researcher may wish to perform additional sensitivity analysis in any of these cases, especially if the result of the CBA is close to zero (using NPV), or the BCR is close to one. Moreover, if certain measures used are contentious sensitivity analysis may be required. Or if a particular cost or benefit that accounts for a large proportion of the overall costs or benefits associated with a project is calculated using a measure which is subject to some sort of arbitrary value or fraction sensitivity analysis may be appropriate.

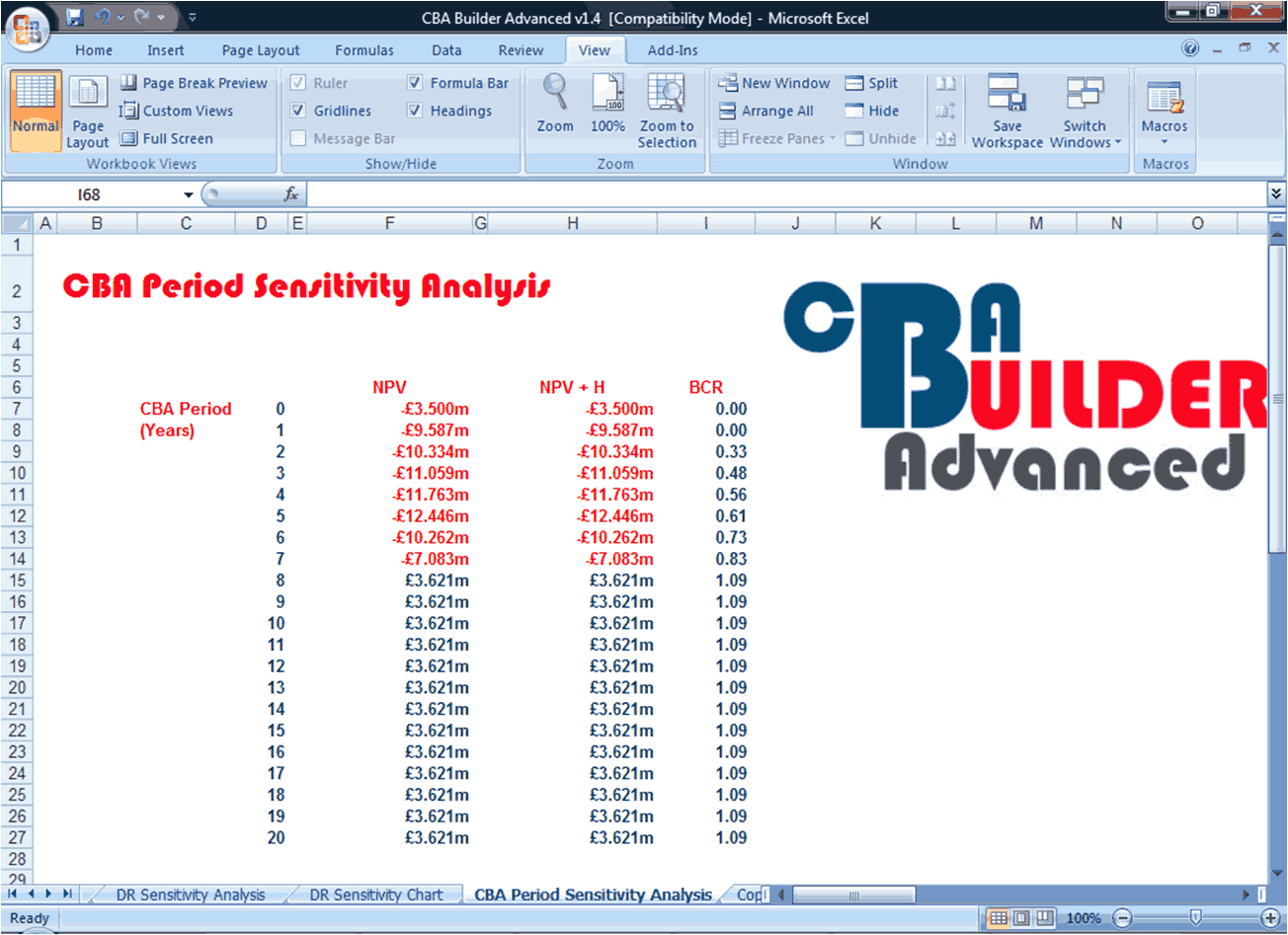
CBA Period Sensitivity Analysis

It is common to use a period of 20 years when evaluating a project. However, this decision could have important consequences on outcomes of project evaluation if some costs or benefits occur in the longer term, or if clients require data on project outcomes at various stages throughout the project period to ascertain the time it takes before they see a return on their investment (this may be particularly important with private sector projects). Horizon values offer one method of addressing longer terms. But what about outcomes within the project period? It may be useful to consider the relative shorter and longer term impacts of a project during the project period using CBA period sensitivity analysis (this can be performed using CBA Builder Advanced). In the simple example shown below, it is not until year 8 of the project period that a positive return (net benefit) is received on the investment. This information could prove especially useful in presenting project outcomes to clients, and when considering a range of project options.

cbaperiod