Horizon Values

Long-term projects and Horizon Values

In some cases the costs or benefits associated with a project may continue to arise years on into the future. Using the standard discounting equation to discount to present value for costs and benefits over multiple years allows the researcher to calculate the present value for any costs and benefits. However, it may prove impractical for the researcher to input values for each and every year for all costs and benefits that continue to occur, especially if some of the costs and benefits continue far into the future. In this case one solution is to use a horizon value. That is, the researcher considers costs and benefits arising close to the beginning of the project, and then separately considers costs and benefits occurring into the far future (horizon).

In this case the researcher would use the following equation:

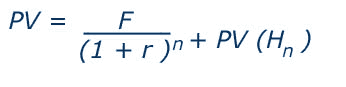
horizon

Where,
FV = future value
P = present value of cost or benefit in monetary terms
r = the rate of discount
n = no. of periods under consideration (e.g. years)
PV (Hn) = the present value of the horizon value

Using this equation the researcher considers the costs and benefits associated with a project in the near future up to n periods using the standard method of discounting over multiple years. Then a single value is added which is equal to the present value of the horizon value, i.e. the present value of the net benefits (or benefits minus costs) at the end of the discounting horizon, sometimes referred to as the terminal value. The length of the near future period is determined by each individual project, and so no standard period exists. Typical period lengths may be determined by the length of time a project can exist for before it requires major maintenance. For example, an enterprise training centre may continue running for 25 years, by which time the building may require substantial maintenance and modernisation, requiring a new project. In this case the near future period would be equal to 25 years, and the horizon value would be a terminal value as the project at that point ceases.

Estimating Horizon Values

A number of methods exist for estimating horizon values. Often researchers will estimate horizon values using a number of methods and then compare the results to attempt to provide additional robustness to the final value which is used in the CBA. The various methods for estimating horizon values are:

(1) Simple projections

This method is similar to standard discounting over multiple years, but distinguishes between the near and far future. The near future is calculated as for standard discounting to present value. The far future is estimated based on the assumption that the benefit or cost will grow or decline at a constant rate. For example, assume we wish to estimate the horizon value of a project. The benefits and costs associated with this project have been calculated for the first 20 years. The net benefit (benefits minus costs) in the 21st year is estimated to be £100,000, and is estimated to continue to grow at a rate of 1% per year, with an interest rate of 5%. We can now use the following formula to calculate the horizon value:

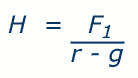
horizon1

Where,
H = horizon value of the net benefit
F = future value of the net benefit
r = the rate of discount (interest rate)
g = the rate of growth or decline

This formula is only appropriate, however, provided the interest rate is greater than the growth rate (i > g). Inputting the net benefits estimated for the project in our example gives:

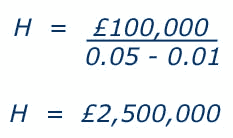
horizon2

This figure represents the horizon value for the project at the end of the 20th year. We can now estimate the present value of this horizon value as follows:

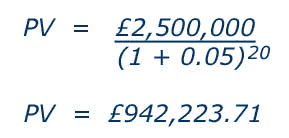
horizon3

(2) Liquidation or Scrap value

In some cases the liquidation value (sometimes referred to as scrap, salvage, terminal or other such term) is used as the horizon value. This method of estimating the horizon value is suitable when no other benefits or costs arise beyond the discounting period, and the project comes to a finish. It also assumes that the market value reflects the wider social value. In reality, however, it may prove difficult to estimate some liquidation values as no market may exist for certain assets e.g. a used road.

(3) Depreciated value

This method allows the researcher to estimate the current value of an asset by subtracting its depreciation from its initial value. The value of most assets declines over time. For example the value of a new car declines as soon as you leave the show room and continues to decline as it ages. The rate of decline or depreciation may be obtained by conducting analysis of the value of similar assets. This method is useful when a liquidation or scrap value is not known for an asset, but a rate of depreciation for the asset (or comparable assets) is known. This method should not be confused with ‘accounting depreciation’ which should not be used in calculating costs or benefits in a CBA.

(4) Initial Construction cost

This method estimates the horizon value as a fraction of the original construction cost. For example, if the construction cost of an enterprise training centre is £5.7m, the horizon value of the training centre may be estimated as 50% of this original construction cost, equal to £2.85m. However, the major concern with this method is in determining the fraction (percentage) figure. This is an arbitrary figure and may not accurately represent the future costs or benefits associated with the project.

(5) Horizon value equal to zero

A final method is to employ a long ‘near future’ discounting period, and assume no costs or benefits after this time. It is equivalent to assuming a zero horizon value. This may be a reasonable assumption in many cases given a suitable near future period is identified. However, for certain government projects, for example a project focusing on improving education in a deprived area through investment in new schools, the impacts of the project may continue far into the future. Using a zero value method in this case may result in important costs or benefits being excluded from the CBA.

Reference

Some of this page is based on Anthony E. Boardman, David H. Greenberg, Aidan R. Vining, David L. Weimer (2011), Cost-Benefit Analysis: Concepts and Practice, Cambridge University Press, pp. 154-155