Discounting and Compounding

Discounting and Compounding

Costs and benefits of projects analysed using CBA rarely occur within a short time period. It is more often the case that at least some of the outcomes of a project occur over time. However, as the value of money changes over time – due to the effects of inflation etc. – the value of a cost or benefit in the future may not be representative of the actual worth of that cost or benefit in present terms. For this reason, it is necessary to discount the future values of costs and benefits occurring over time to a common metric – present values. This also allows researchers to calculate the net present value of a project.

Discounting to present value

Discounting to present value involves calculating the current equivalent value of a cost or benefit associated with a project, given a prevailing interest (or discount) rate. The current equivalent monetary value of a cost or benefit that will be received in the future is called its present value. The formula used to calculate the present value of a future cost or benefit in monetary terms is:

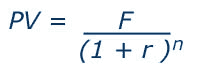
discount

Where,
PV = present value
F = future value of cost or benefit in monetary terms
r = the rate of discount
n = no. of periods under consideration (e.g. years)

Click here for a simple discounting example

Discounting over multiple years

In some cases the costs or benefits associated with a project occur over multiple years. In this case discounting the future values of any such costs and benefits becomes a particularly important part of any CBA if it is to provide an accurate net present value of a project. The formula used to calculate the present value of future costs or benefits in monetary terms over multiple years is:

multiyear1

Or,

multiyear

Example

Consider a project which produces an income of £2000 for four years. At the end of this period a piece of machinery involved in the project is then sold for scrap for £500. Assume a discount rate of 10% (or 0.10). To calculate the present value of these future benefits we use the above equation as follows:

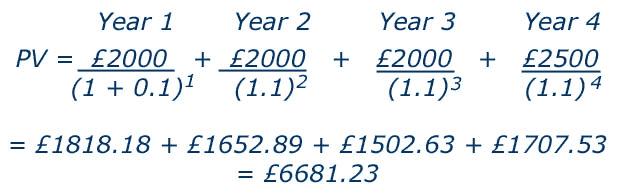
multiyear2

More multiple year discounting examples

Discounting Rates

An important consideration when discounting future costs and benefits to present value is the discount rate applied. In the UK the Green Book: Appraisal and Evaluation in Central Government produced by HM Treasury recommends a discount of rate of 3.5% (HM Treasury, 2011, 26). The Green Book discount rate is generated using the following equation:

r = ρ + µg

Where,
r is the discount rate.
ρ is pure time preference (discount future consumption over present consumption on the basis of no change in expected per capita consumption).
µ is elasticity of marginal utility of consumption
g is annual growth in per capita consumption

The ‘time preference’ comes from the principle that, generally, people prefer to receive goods and services now rather than later. Meanwhile, the latter part of the equation refers to the fact that growth means people are better off and extra consumption worth less. This reflectsthat future consumption will be plentiful relative to the current position and thus will generate lower marginal utility (HM Treasury, 2011, 97).

HM Treasury assume that ρ = 1.5%, µ = 1 and g = 2% so that:

0.015 + (1*0.02) = 0.035 = 3.5%

In addition, the Green Book provides recommendations for reducing the discount rate applied for projects which exceed a 30 year period (HM Treasury, 2011, 99). The long term discount rates recommended are as follows:

Period (in years)	0-30	31-75	76-125	126-200	201-300	301+
Discount rate	3.5%	3.0%	2.5%	2.0%	1.5%	1.0%

Note, also, that while the discount rate of 3.5% is recommended by UK Government other discount rates are used commonly in evaluation projects. The Stern Review of Climate Change (2006) assumes ρ=0.1%, µ=1 and g=1.3% generating a discount rate, r=1.4%. This is controversial, but in essence applies a greater weighting to future costs/benefits.

Future Values or Compounding

In some cases estimates of the present value of costs or benefits may be known and future values may be required. For example, if you wish to estimate the value of an investment involved in a project in one years time given a known rate of interest. To calculate the future value of a cost or benefit you would use the following equation:

Where,
FV = future value
P = present value of cost or benefit in monetary terms
r = the rate of discount
n = no. of periods under consideration (e.g. years)

The present value being considered, denoted by P, is invested for n years with a compound interest rate of r percent per period (usually years). In this equation the term (1 + r)^n is sometimes referred to as the compound interest factor. This term is used in textbooks and is included as a function on most spreadsheet programs and some calculators.

Problems with Discounting

A key concern involved in the use of discounting is the value assigned to the discount rate. An incorrect value for the discount rate could easily result in an inaccurate estimate of the present value of a future cost or benefit, and equally could result in the CBA of an entire project providing an inaccurate net present value. Often government agencies provide a suggested discount rate to use when performing discounting. For example, the rate specified in the UK by HM Treasury for researchers to use when calculating present values of costs and benefits.

A second limitation in the common method of discounting to present value is in the timing of costs and benefits. The standard method of discounting future costs and benefits to present values assumes that all costs and benefits occur at the end of each year (or at least uses this timing for ease of calculation). However, it may be that in some cases the timing of costs and benefits needs to be considered more minutely. If a cost occurs half way through a year its discounted value may be different, albeit possibly not by that much, than if the value is discounted at the end of the year. Depending on the overall length of a project, in reference to the costs and benefits arising from it, the timing of the discounting periods may need to be adjusted. For example instead of using 1, 2, 3, 4, 5 etc. a researcher may deem it more appropriate to use 1, 1.5, 2, 2.5, 3 etc.

Sources of Disagreement over Discount Rates

(adapted from Stiglitz, 2000, 288)

	High Discount Rate (Opportunity Cost of Capital)	Low Discount Rate (Social Discount Rate)
1	Government investment needs tend to result in the displacement of private investment.	Assessing net impacts is typically more complex than simply assuming that £1 of public expenditure displaces a £1 of private investment.
2	Even in a world with distortions, everyone could be better off if efficiency is maintained. This however, requires that the rate of return on public projects is the same as that on private projects.	Assessing the desirability of a project must take into account intergenerational distributional effects as well as efficiency effects. Those who receive the benefits from a project are often different from those who bear the costs. Even if it were possible for governments to make everyone better off, the required compensation to do so is rarely received by all those affected (especially those adversely affected).
3	Even in the absence of government intergenerational redistributions, if children receive inheritance from their parents, marginal valuations of consumption between generations will be equal (the dynastic model).	In the absence of optimal intergenerational redistribution, market interest rates do not accurately reflect marginal social valuations of money (£) to different generations. The dynastic model is questionable.
4	When market distortions are caused by optimal taxes, efficiency is still desirable, so the government should use the opportunity cost of capital as the discount rate.	With market distortions, marginal rates of substitution (the value of a marginal £1 in different years) and marginal rates of transformation (the trade-offs facing firms) may differ markedly. With distortionary taxes, efficiency is desirable only under certain restrictive conditions.